关于统计

1.正态分布与置信区间

假如有一列数：

A=[0.951096912722347   0.950813889320115         0.932576649756777         0.932405277230298         0.933804895447660                0.932772384405534         0.934919429111776         0.934268797790927         0.951949040237572         0.951813399650483                0.950900669288437         0.965204871494392         0.940041317132878         0.901790772297916         0.882272236610862                0.880197853556540         0.990825707790875         0.946486935002587         0.975909396820861         0.955673876178256                0.952257015437101         0.953329199413195         0.967097647570643         0.946430719563458         0.953413230724527                0.949185329921404         0.953997918787625         0.986266708192098         0.946775561296547         0.955059809589028                0.967324086145567         0.946423534679043         0.965064918853927         0.958524186188790         0.958331971162011                0.960700539729026         0.960167317142403         0.966710927412354         0.961033326373741         0.969854059868902                0.978689688261696         0.982955728679599         0.960999967008962         0.968491612968834         0.955723550385393                0.990520358902372         0.950883959373629         0.972036914356757         1.00139728047903            0.948625094415445                0.956527525862292         0.969123458648294         0.976604507889189         0.962493281173283         0.960637099653849                0.965849046307893         0.973086479138527         0.975290796923871         0.976516491927757         0.975202076220499                0.976964071038427         0.951924949534533         0.924440118733620]’;

想要得到平均值mean，用mean(a);

想要得到标准偏差stand deviation,用std(a);

想要得到柱状图及最匹配的正态分布，用histfit(a);xlable(‘values’);ylable(‘number of events’);

想得到概率分布函数probability density functions(PDF),用pdf=normpdf(a, mean(a), std(a));plot(a, pdf);

 

想要的到变量a的概率分布为0.025和0.975的值，用norminv([0.025, 0.975], mean(a), std(a));

这就得到了95%的置信区间。

 

不知道标准偏差的情况下，估计平均值；

N=length(a);

alpha=0.025 % choose the significance level;

u=-tinv(alpha/2, N-1);

x_bar=mean(a);

sigma=std(a);

ConfidenceInterval=[ x_bar-u*sigma/sqrt(N), x_bar+u*sigma/sqrt(N)]

 

另外一种，直接计算95%概率的分布区间：

quantile(c1,0.025)  % 2.5%频率时的值

quantile(c1,0.975)  % 97.5%频率时的值

 

伯尔尼大学应用学科（ Bern University of Applied Sciences）的Andreas Stahel在《用Matlab/Octave进行统计》讲得非常好，附上链接。

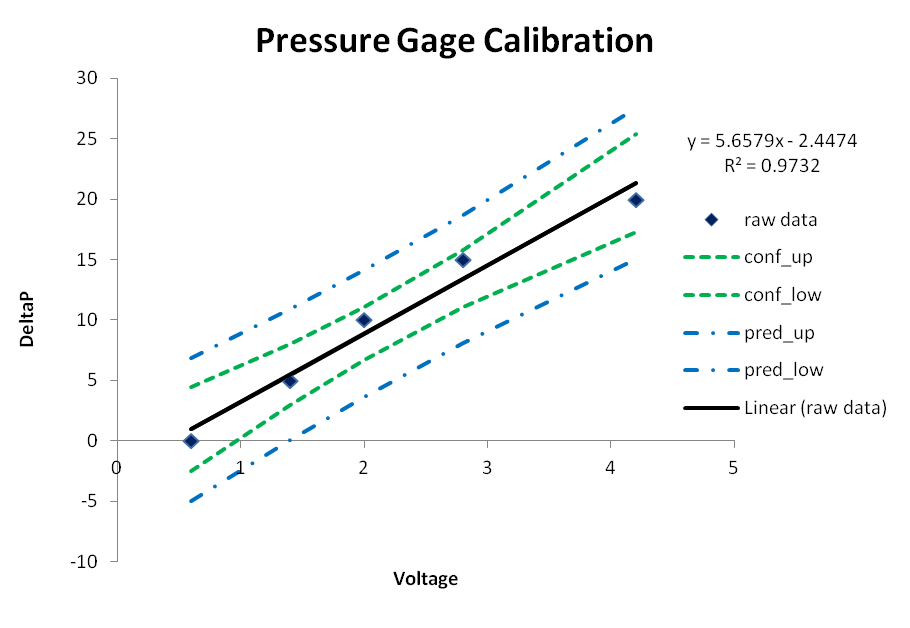
2.线性最小而成回归的预测与置信区间

例如有一组变量：

y	x
DeltaP	V
0	0.6
5	1.4
10	2
15	2.8
20	4.2

要进行回归并计算95% 的置信区间，可以用excel进行，参见https://youtu.be/aSOUQKqIYak；

也可以手算，或者用R计算，参见https://youtu.be/qVCQi0KPR0s；

我觉得第二个视频中讲得正确一些，第一个视频的结果是做了某些程度的化简。

其实用R感觉蛮简洁的，

> m1=lm(y~x)

> summary(m1)

 

Call:

lm(formula = y ~ x)

 

Residuals:

1       2       3       4       5

-0.9474 -0.4737  1.1316  1.6053 -1.3158

 

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept)  -2.4474     1.3682  -1.789  0.17160

x             5.6579     0.5425  10.429  0.00188 **

—

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

 

Residual standard error: 1.496 on 3 degrees of freedom

Multiple R-squared:  0.9732,    Adjusted R-squared:  0.9642

F-statistic: 108.8 on 1 and 3 DF,  p-value: 0.001882

> predict(m1,1.3,interval='confidence')

fit       lwr       upr

1  0.9473684 -2.540034  4.434771

2  5.4736842  2.936226  8.011142

3  8.8684211  6.711997 11.024846

4 13.3947368 11.027450 15.762024

5 21.3157895 17.259383 25.372196

 

> predict(m1,interval='prediction')

fit         lwr      upr

1  0.9473684  -4.95319353  6.84793

2  5.4736842  0.07985908  10.86751

3  8.8684211  3.64301926  14.09382

4  13.3947368  8.07884517  18.71063

5  21.3157895  15.06206316  27.56952